Decision Tree와 Random Forest 완벽 정리
원리, 장단점, 비교, 실무 활용까지
결정트리(Decision Tree)는 직관적이고 해석이 쉬운 모델이지만 과적합에 취약합니다. 랜덤 포레스트(Random Forest)는 여러 트리를 결합(앙상블)해 안정적인 성능을 내며 실무에서 매우 널리 사용됩니다.
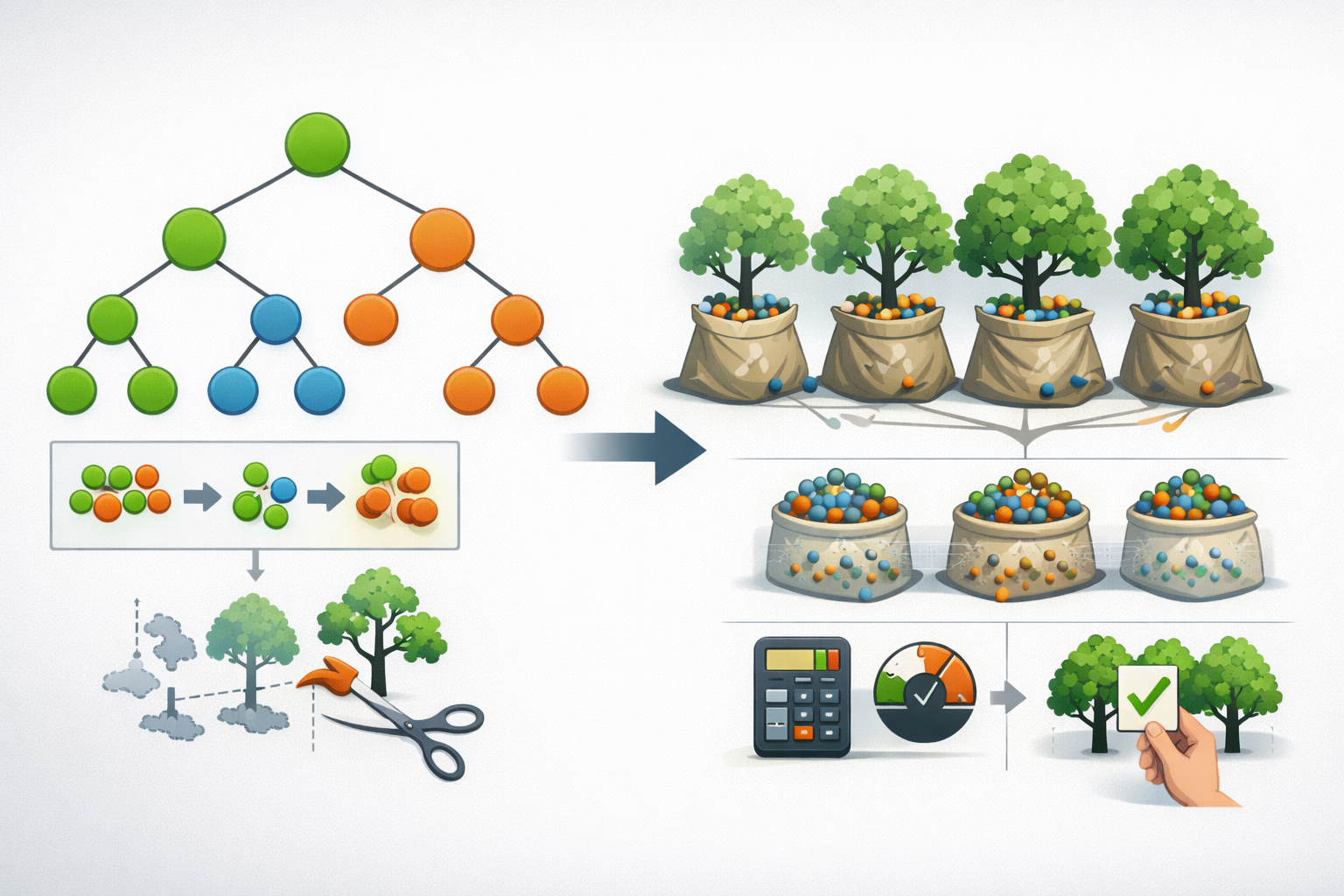
I. Decision Tree(결정트리)란?
Decision Tree는 데이터를 “질문(조건)”으로 나누며 학습하는 트리 기반 모델입니다. 루트 노드에서 시작해 내부 노드에서 조건 분기(split)를 반복하고, 최종적으로 리프 노드(leaf)에서 예측값을 출력합니다.
핵심 직관: “가장 잘 구분되는 질문을 먼저 던지고, 그 다음 질문을 이어가며 데이터를 점점 더 순수(동일 클래스 또는 유사한 값)하게 만든다.”
1. 결정트리의 구성 요소
- Root node: 첫 번째 분기 기준
- Internal node: 중간 질문 노드(조건 분기)
- Leaf node: 최종 예측(클래스 또는 수치)
- Depth: 트리의 깊이(복잡도와 직결)
2. 결정트리 예시(개념)
소득 > 5천만원?
├─ Yes → (신용등급 A)
└─ No
├─ 나이 > 35?
│ ├─ Yes → (신용등급 B)
│ └─ No → (신용등급 C)위처럼 ‘조건’을 따라가며 최종 예측에 도달합니다.
II. 결정트리의 분할 기준: 불순도/분산 감소
결정트리 학습의 핵심은 “어떤 기준으로 데이터를 나누면 가장 잘 구분되는가?”를 찾는 것입니다. 이때 분류(Classification)와 회귀(Regression)에 따라 사용되는 기준이 다릅니다.
1. 분류 트리: 불순도(Impurity) 감소
분류 트리는 노드 안의 클래스가 “섞여 있을수록” 불순도가 높고, “한 클래스에 몰릴수록” 불순도가 낮습니다. 학습은 분할 전 → 분할 후 불순도 감소량이 최대가 되도록 split을 선택합니다.
- Gini: \( Gini = 1 - \sum p_i^2 \)
- Entropy: \( Entropy = -\sum p_i \log p_i \)
- Information Gain: 분할로 줄어든 Entropy(또는 Gini)만큼의 이득
2. 회귀 트리: 분산(또는 MSE) 감소
회귀 트리는 목표값(y)이 노드 내부에서 얼마나 “흩어져 있는지”를 기준으로 나눕니다. 보통 분산 또는 MSE가 가장 크게 줄어드는 split을 택합니다.
- 분산: \( Var = \frac{1}{n}\sum (y_i - \bar{y})^2 \)
- MSE: 예측 오차 제곱의 평균
- 목표: 분할 후 각 리프에서의 오차를 최소화
요약: 분류는 “클래스가 더 깔끔히 분리되는 분할”, 회귀는 “값의 흩어짐이 줄어드는 분할”을 선택합니다.
III. 결정트리 장단점 & 과적합 방지(Pruning)
1. 결정트리 장점
- 해석력: 규칙 기반으로 설명 가능(Explainable)
- 전처리 부담 낮음: 스케일링 필수 아님
- 비선형 관계 및 상호작용을 자연스럽게 포착
- 변수 중요도 파악이 비교적 쉬움
2. 결정트리 단점(핵심)
- 과적합에 매우 취약 (깊이가 깊어질수록)
- 데이터의 작은 변화에도 트리 구조가 크게 바뀔 수 있음(불안정)
- 단일 트리 성능의 한계
실무에서는 “설명 목적”이 아니라면 결정트리 단독 사용보다 앙상블(랜덤 포레스트/부스팅)을 더 많이 선택합니다.
3. 과적합 방지 방법(가지치기/제한)
- max_depth: 트리 최대 깊이 제한
- min_samples_split: 노드를 쪼개기 위한 최소 샘플 수
- min_samples_leaf: 리프 노드 최소 샘플 수
- pruning: 사후 가지치기(복잡도 줄이기)
IV. Random Forest(랜덤 포레스트)란?
Random Forest는 여러 개의 결정트리를 만들고, 그 예측을 평균(회귀) 또는 다수결 투표(분류)로 결합하는 앙상블 모델입니다. 결정트리가 가진 “불안정성(높은 분산)”을 줄이는 것이 목표입니다.
한 줄 정의: “서로 다르게 학습된 결정트리들을 여러 개 만들고, 결과를 합쳐 더 안정적이고 성능 좋은 예측을 만든다.”
예측 방식
- 분류: 트리들의 예측 클래스 중 다수결(Majority Voting)
- 회귀: 트리들의 예측값 평균
회귀 예측(개념):
y_hat = (y_hat_tree1 + y_hat_tree2 + ... + y_hat_treeT) / T
V. 랜덤 포레스트의 핵심: 2가지 랜덤성
랜덤 포레스트는 트리들을 “서로 다르게” 만들기 위해 랜덤성을 주입합니다. 트리들이 서로 비슷하면 앙상블 효과가 줄어드므로, 트리 간 상관을 낮추는 것이 중요합니다.
1. Bootstrap Sampling (데이터 랜덤)
- 원 데이터를 중복 허용으로 랜덤 샘플링
- 각 트리는 서로 다른 샘플 세트로 학습
- 일종의 Bagging(bootstrap aggregating)
2. Feature Randomness (특성 랜덤)
- 각 노드 split에서 전체 feature 중 일부만 후보로 선택
- 특정 강력한 변수가 모든 트리를 똑같이 지배하는 현상을 완화
- 결과적으로 트리 간 다양성↑, 일반화 성능↑
효과: 랜덤 포레스트는 결정트리의 분산(Variance)을 크게 줄여 과적합에 강하고 예측이 안정적입니다.
VI. 주요 하이퍼파라미터 정리
트리 기반 모델은 하이퍼파라미터가 모델 복잡도와 직결됩니다. 아래 표를 “튜닝 체크리스트”로 활용하면 좋습니다.
| 파라미터 | 적용 | 의미 | 튜닝 포인트 |
|---|---|---|---|
| max_depth | DT / RF | 트리 최대 깊이 | 깊을수록 과적합↑, 얕을수록 성능↓ 가능 |
| min_samples_split | DT / RF | 노드를 split하기 위한 최소 샘플 수 | 값을 키우면 과적합 완화 |
| min_samples_leaf | DT / RF | 리프 노드 최소 샘플 수 | 값을 키우면 결정 경계가 부드러워짐 |
| n_estimators | RF | 트리 개수 | 많을수록 안정적이지만 학습/추론 비용↑ |
| max_features | RF | 각 split에서 고려할 feature 수 | 작게 하면 다양성↑(상관↓), 너무 작으면 성능↓ |
| bootstrap | RF | 부트스트랩 샘플링 사용 여부 | 일반적으로 True가 기본 |
VII. Decision Tree vs Random Forest 한눈에 비교
| 항목 | Decision Tree | Random Forest |
|---|---|---|
| 해석력 | 매우 높음 (규칙 기반) | 상대적으로 낮음 (트리 다수) |
| 성능(일반화) | 중간~낮음 (과적합 위험) | 높음 (분산 감소) |
| 과적합 | 취약 | 강함 |
| 안정성 | 데이터 변화에 민감 | 상대적으로 안정적 |
| 실무 활용 | 설명 목적/룰 기반에 적합 | 강력한 기본 모델(베이스라인)로 널리 사용 |
VIII. 언제 무엇을 써야 할까?
1. Decision Tree가 유리한 상황
- 설명 가능성이 최우선(규제 산업, 의사결정 근거 필요)
- 규칙 기반 정책/룰을 만들고 싶을 때
- 모델 교육·설명·프로토타이핑 용도
2. Random Forest가 유리한 상황
- 성능과 안정성이 중요한 실무
- 비선형 관계, 변수 간 상호작용이 강한 문제
- 튜닝 부담이 비교적 낮은 강력한 베이스라인이 필요할 때
[칼럼 - 이규철] AI교과서(34) - 의사결정 나무와 랜덤 포레스트(Decision Tree/Random Forest) - 한국AI부동
▲이규철/한국공공정책신문 칼럼니스트 ⓒ한국공공정책신문 [한국공공정책신문=김유리 기자] ◇ 의사결정 나무의 개념의사결정나무(木)ㆍ랜덤포레스트(Decision Tree/Random Forest)에서 의사결정나
www.kairnews.com
IX. 실무 팁: 성능·해석·운영 관점
1. “단독 트리”는 조심해서 사용
결정트리는 이해하기 쉽지만, 깊이가 커지면 학습 데이터에만 과도하게 맞춰지는 경향이 큽니다. 실무 성능이 목적이라면 랜덤 포레스트 또는 그 이후의 부스팅 계열(XGBoost/LightGBM 등)도 함께 고려하는 편이 안전합니다.
2. 변수 중요도(Feature Importance)는 참고하되 해석은 신중히
랜덤 포레스트는 변수 중요도를 제공하지만, 데이터 특성(상관 변수, 범주형 인코딩 방식 등)에 따라 중요도 해석이 왜곡될 수 있습니다. 중요도를 “절대적인 인과”로 해석하기보다는, 탐색적 인사이트로 활용하는 것을 추천합니다.
3. 속도/비용 고려
랜덤 포레스트는 트리 수(n_estimators)가 많아질수록 예측이 안정적이지만, 학습/추론 비용도 증가합니다. 서비스 운영 환경에서는 트리 수와 깊이를 함께 조절해 정확도 vs 비용의 균형을 잡는 것이 중요합니다.
결론 한 줄: Decision Tree는 “이해를 위한 모델”, Random Forest는 “실제로 쓰기 좋은 모델”입니다.
'인공지능' 카테고리의 다른 글
| AI 친화적인 프롬프트 작성 노하우: Role·Instruction·Goal·Context부터 고급 테크닉 7가지까지 (0) | 2026.01.31 |
|---|---|
| ChatGPT 5.2 출시: GPT 버저닝 업그레이드 역사와 개선 방향 총정리 (0) | 2026.01.22 |
| TensorFlow란? 개념부터 학습·배포 생태계까지 한 번에 정리 (0) | 2026.01.22 |
| 딥시크 AI가 사용하는 전문가 혼합(MoE) 방식이란? 원리부터 장단점까지 완벽 정리 (0) | 2026.01.22 |
| AI가 글자를 이해하는 단위, 토큰(Token)이란 무엇인가? (0) | 2026.01.22 |



